2つの物体の衝突で力学的エネルギー保存則は使えるか?では、2つの物体が互いに衝突する運動において、力学的エネルギーが保存されない例を挙げました。
しかし、このような運動でも、力学的エネルギーが保存されるケースがあります。
それは、質量が同じ2つの物体が「弾性衝突」をした場合です。
弾性衝突とは?
物体の衝突と反発係数でも紹介していますが、弾性衝突とは、反発係数(=e)が1となる衝突です。
(参考書によっては、「完全弾性衝突」と記載されているものもありますが、意味は同じです。)
なお反発係数とは、物体間の跳ね返りの度合いを示すもので、必ず0≦e≦1の範囲を取ります。
反発係数が0の場合だと、例えば真上から落とした物体が他の物体の上にぶつかっても全く跳ね返りません。そのまま止まります。
つまり反発係数が1ということは、言い換えればぶつかった時に最もよく跳ね返るということです。
具体例
今、質量がともに\(m\)の二つの物体A、Bがあり、一直線上を水平に、それぞれ速度\(v\)、\(-v\)で運動しています。
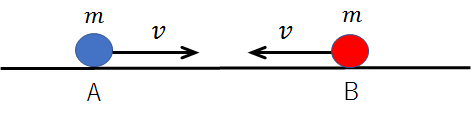
※速度と速さは別物なので注意してください。速度は大きさと向きをもった量なので、マイナスがつくということは向きが逆ということです。
(具体例の図では、右向きが正の向きということになります。)
一直線上の水平運動であることから位置エネルギーは変化しないため、運動エネルギーのみを考慮すると、
衝突前における、それぞれの物体の力学的エネルギーは、
物体A・・・\(\frac{1}{2}mv^2\)
物体B・・・\(\frac{1}{2}m(-v)^2\)
よって、衝突前の力学的エネルギーの総和は、
\(\frac{1}{2}mv^2\)+\(\frac{1}{2}m(-v)^2\)
=\(mv^2\)・・・・・(1)
次に、この2つの物体が弾性衝突をしたとして、運動量保存則の式と反発係数の式を、それぞれ立ててみます。
衝突後のそれぞれの物体の速度を\(v_A\)、\(v_B\)とすると、運動量保存則より、
\(mv\)+\(m(-v)\)=\(mv_A\)+\(mv_B\)・・・・・(2)
反発係数の式より、
-\(\frac{v_A-v_B}{v-(-v)}\)・・・・・・(3)
(2)より、\(v_B\)=-\(v_A\) であるから、これを(3)に代入すると、
-\(\frac{2v_A}{2v}\)=1
ゆえに、\(v_A\)=-\(v\)、\(v_B\)=\(v\)となります。
つまり、衝突後の物体AとBは、同じ速さで互いに逆向きに離れていくことがわかります。
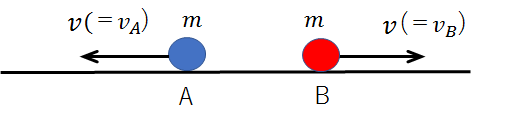
この時のそれぞれの物体の力学的エネルギーは、
物体A・・・\(\frac{1}{2}m(-v)^2\)
物体B・・・\(\frac{1}{2}mv^2\)
よって、衝突後の力学的エネルギーの総和は、
\(\frac{1}{2}m(-v)^2\)+\(\frac{1}{2}mv^2\)
=\(mv^2\)・・・・・(4)
(1)の結果と同じになります。
したがって、質量が同じ2つの物体が「弾性衝突」をした場合、運動量も力学的エネルギーも保存されます。
衝突したことで物体に保存力以外の力がはたらいているので、本来力学的エネルギーが保存される条件ではないはずですが、これは特別なケースと言えるでしょう。