質量\(m\)の小物体が、滑らかな床面を水平右向きに速度\(v\)で運動している。
この小物体が床面の端に到達したのち、質量\(M\)、動摩擦係数\(μ\)の静止している台車の上に移動し、その後一体となって運動した。
この時の速度を求めよ。
ただし、台車が置かれている床面も滑らかであり、小物体が滑っていた床面と台車との間に隙間は無いものとする。

小物体には、台車の上に乗った瞬間から摩擦力がはたらきます。
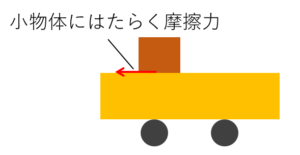
これにより小物体の速度は徐々に小さくなり、最終的に台車上で静止します。
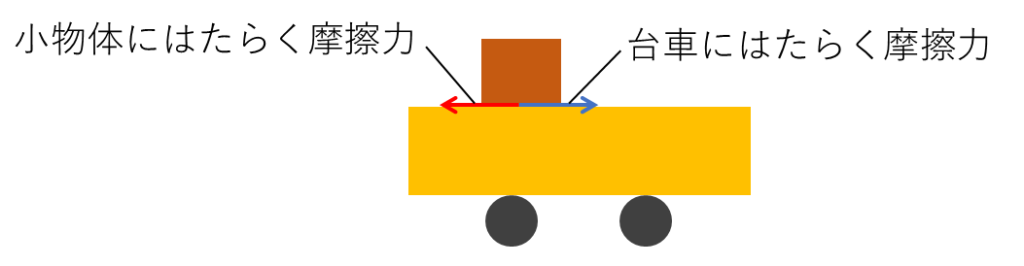
ですが、小物体にはたらく摩擦力と同じ逆向きの力が台車にもはたらくことで、台車(と小物体)は右向きに運動します。
この関係は「作用・反作用」といいます。
ちなみに、小物体が移る前は台車は静止しているので、速度はゼロですね。
よって、求める速度を\(V\)とすると、運動量保存則より、
\(m・v+M・0=(m+M)・V\)
∴\(V\)=\(\Large\frac{mv}{m+M}\)
となります。
----------------------------------
シンプルな答えになりますが、スムーズに「運動量保存則」が浮かびましたでしょうか?
実はこの手の問題、つい誤って力学的エネルギー保存則を使って解いてしまう人が多いんですが、
残念ながらこの法則は使えません。
なぜならこの状況では、力学的エネルギーが保存されていないからです。
2つの物体の衝突で力学的エネルギー保存則は使えるか?でも紹介した通り、力学的エネルギー保存則が使えるのは、
○物体に保存力以外の力がはたらいていても、それらの力のする仕事がゼロ
この二つの場合です。
保存力とは、重力、弾性力、静電気力などのことで、今回発生する摩擦力は該当しません。
更に摩擦力のした仕事もゼロではありません。小物体を静止させたり、台車を動かすために仕事をしていますよね。
----------------------------------
今一度運動量保存則について挙げてみます。
物体系が内力を及ぼしあうだけで外力を受けていないとき、全体の運動量の和は一定に保たれる。
今回のケースでは、小物体が台車に乗っかってから一緒に滑り出すまでの間、互いに及ぼしあった摩擦力が内力に相当します。
そして小物体も台車も、外部から余計な力は受けていません。
したがって、小物体と台車をひっくるめた運動量の和は一定に保たれているので、運動量保存則が使えます。
運動量保存則も力学的エネルギー保存則も便利な法則ですが、それぞれ使える条件が決まっているので、間違えないようにしてください。