滑らかな台の上から小球を速さ\(v_0\)で水平投射したところ、水平より\(θ\)だけ角度をつけた状態で床の上に落下した。

この時、投射位置の床からの高さと、小球が落下した地点の投射位置からの水平距離をそれぞれ求めよ。
なお、台は床の上に鉛直に立っており、水平方向右向き及び鉛直方向下向きをそれぞれ正とする。
水平投射の基本問題です。
ばねの勢いで水平に投射する運動で扱った問題と似ていますが、今回は求めるものが違います。
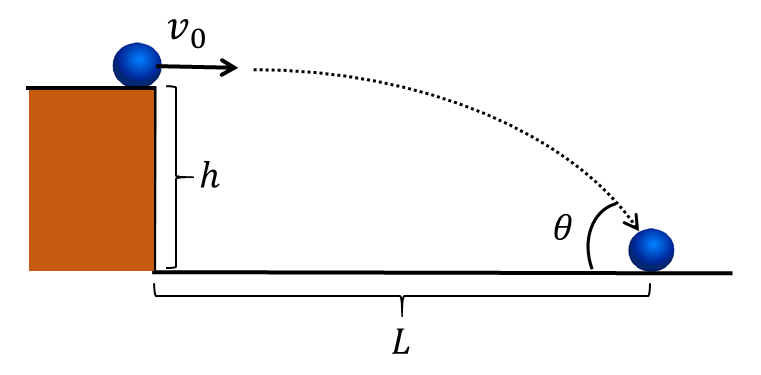
図中に示すと、\(h\)と\(L\)の部分となります。
\(h\)は「鉛直方向に進んだ距離」、\(L\)は「水平方向に進んだ距離」ですね。
水平投射の記事でも紹介していますが、水平投射における物体の運動は水平方向と鉛直方向に分解することができ、水平方向は等速直線運動、鉛直方向は自由落下として考えることができます。
今回は投射してから床の上に到達するまでの時間を求め、それを使ってそれぞれの距離を求めてみましょう。
---------------------------------
まず小球が床に到達した時点の速度を\(v\)とし、これを水平方向の成分\(v_x\)と鉛直方向の成分\(v_y\)に分解します。
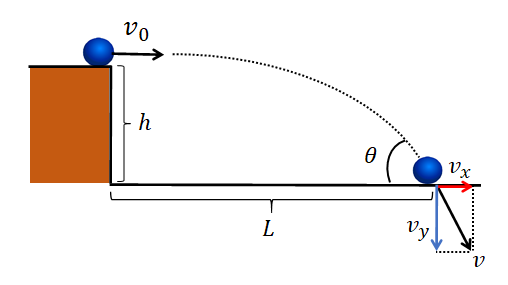
投射してから床の上に到達するまでの時間を\(t\)とすると、\(t\)秒後のそれぞれの速度成分は、
\(v_x=v_0\)(等速直線運動なので速度は不変)
\(v_y\)=\(gt\)(\(g\)は重力加速度。自由落下の公式による)
となります。
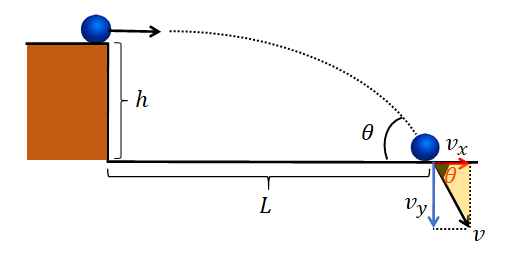
ここで、上図の薄黄色の三角形に注目すると、三角比の公式より、
\(\tanθ=\Large\frac{v_y}{v_x}=\Large\frac{gt}{v_0}\)
\(t=\Large\frac{v_0tan θ}{g}\)
これで、投射してから床の上に到達するまでの時間を表すことができました。
よって、鉛直方向は自由落下の変位の式を用いて、
\(h=\Large\frac{1}{2}\)\(gt^2\)\(=\Large\frac{g}{2}×\Large\frac{v_0^2{\tan^2θ}}{g^2}=\)\(\Large\frac{v_0^2{\tan^2θ}}{2g}\)
水平方向は等速直線運動なので「速さ×時間」の公式より、
\(L=v_0t=\)\(\Large\frac{v_0^2{\tanθ}}{g}\)
となります。
---------------------------------
繰り返しになりますが、水平投射における物体の軌道は、水平方向と鉛直方向の運動が組み合わさったものです。
このため、ある地点に到達するまでの時間がわかれば、それを使って水平方向と鉛直方向それぞれの距離を求めることができるのです。