力学的エネルギーが保存されない運動

「保存力」と「力学的エネルギー保存則」で紹介した力学的エネルギー保存則とは、下記のようなものでした。

物体に保存力のみがはたらいている場合、その物体の力学的エネルギーは一定である。

物体に保存力以外の力がはたらいていても、それらの力のする仕事がゼロの場合、その物体の力学的エネルギーは一定である。

つまり、力学的エネルギーが保存されない運動の条件は、この逆になります。

物体に保存力以外の力がはたらいており、それらの力のする仕事がゼロではない場合、その物体の力学的エネルギーは一定ではない。

この保存力ではない力を物理用語で「非保存力」といいい、代表的なものが摩擦力です。

今回は、この摩擦力がはたらく運動について、具体的に見ていきましょう。

あらい斜面上の運動

図のように、あらい水平面上を質量\(m\)の物体が運動する状況を考えます。

重力加速度を\(g\)として運動中の物体にはたらく力を図示すると、下記のようになります。

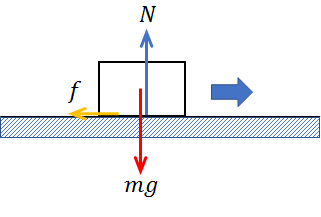
\(mg\)・・・・・重力
\(N\)・・・・・垂直抗力
\(f\)・・・・・動摩擦力

物体は運動しているので、進行方向と逆向きに動摩擦力がはたらいています。

動摩擦力は名前のとおり摩擦力ですから、物体には保存力以外の力がはたらいていることになります。

次に、この物体が距離\(L\)だけ滑ったとしましょう。

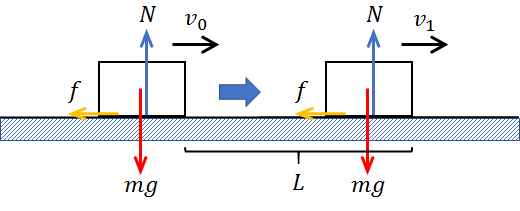
動摩擦力がはたらいているので、距離\(L\)だけ滑る間に物体は減速していきます。

このため、滑り始めの物体の速度を\(v_0\)、距離\(L\)だけ滑った後の速度を\(v_1\)とし、運動エネルギーの大小を比較すると、\(\Large\frac{1}{2}\)\(mv_0^2\)＞\(\Large\frac{1}{2}\)\(mv_1^2\)となります。

なお、\(L\)だけ滑る前と後で物体の高さは変わりませんから、重力による位置エネルギーは変化しません。

よって、滑った後の物体の力学的エネルギーは減少しており、力学的エネルギーが保存されていないことがわかります。

-------------------------

もうひとつ、力学的エネルギーが保存されない条件に、「保存力以外の力がする仕事がゼロではない」というものがありましたね。

先述したように、物体が\(L\)だけ移動する間、ずっと動摩擦力がはたらいていたとなると、動摩擦力は物体に仕事をしたことになります。

ある力がした仕事は、(力の大きさ)×(力の向きへの移動距離)なので、動摩擦力が物体にした仕事は、\(－fL\)となります。

※マイナスがついているのは、動摩擦力が、物体の進行方向と逆向きにはたらくからです。

摩擦のある面を運動すると力学的エネルギーが保存されない(減る)ことがわかりましたが、減ったエネルギーはどこへ消えたのでしょうか？

実は、減った分は動摩擦力がした仕事分としてカウントされたのです。

動摩擦力が仕事をしたことで物体の力学的エネルギーが減ったのであれば、逆に言えば、物体が自身の力学的エネルギーを、動摩擦力が仕事をするためのエネルギーとして与えたとも考えられます。

物体に非保存力がはたらいている場合、物体の力学的エネルギーの差分は、非保存力がした仕事となる。

以上のことを式で表すと、次のようになります。

(\(L\)だけ滑った後の力学的エネルギー)－(滑る前の力学的エネルギー)＝(動摩擦力が物体にした仕事)

⇒\(\Large\frac{1}{2}\)\(mv_1^2\)－\(\Large\frac{1}{2}\)\(mv_0^2\)＝\(－fL\)

以上のことから、例え物体の力学的エネルギーが減ったとしても、その分が動摩擦力がした仕事になったのであれば、運動全体のエネルギーの総和は変わっていないことがわかります。

これを「エネルギー保存の法則」といいます。

今回取り上げた力学的エネルギー以外にも、私たちの身近には、熱によるエネルギー、電気によるエネルギーなど、様々なエネルギーがあります。

例えば風力発電は風の力で電気エネルギーを産み出しますが、単に風のエネルギーが電気エネルギーに変換されただけの話です。

力学的エネルギーが保存されないからと言って、運動に関係するエネルギー全体のバランスが崩れているわけではないことを、覚えておいてください。